In part one of this miniseries, I introduced you to the topic of machine learning. And in part two, I showed you how to get started on a simple Python machine learning project using CrateDB, Jupyter Notebook, and Pandas.
If you followed along with the tutorial in part two, you should have a local CrateDB instance running, some test data (imported tweets from Twitter), and a Jupyter document.
In this post, I am going to show you how to predict the number of Twitter followers a user has using regression analysis.
Why regression analysis?
Well, in the loan approval example we looked at in part one, classification is used to predict discrete values (e.g., "Loan Approved" or "Loan Denied").
Regression analysis, on the other hand, allows you to predict continuous values, i.e. numbers, such as someone's follower count.
(If you want to learn more about the difference between discrete values and continuous values, I recommend that you check out The Elements of Statistical Learning and the corresponding YouTube videos.)
The rest of this post covers the following process:
- Design the experiment
- Load the data
- Explore the data
- Preprocess the data
- Establish a base model
- Establish a linear regression model
- Compare the results
Let's dive in!
Design the Experiment
Here are some important questions to answer when designing an experiment:
- What is your task?
- What is your hypothesis?
- How will you measure the success of the hypothesis?
- What are your independent variables?
- What are your dependable variables?
- What is your control environment?
Let’s go through the process of answering these questions for the experiment we're going to conduct.
Identify The Task
We want to predict the number of followers a Twitter user has by looking at the number of people they follow.
State The Hypothesis
Our hypothesis:
The linear regression model performs better than the base model.
A base model (also called baseline) is a result of a different, usually more naïve, model that we are trying to beat. This serves as a reference against which we can compare the results of the linear regression model.
For something as basic as the experiment we are conducting with our test Twitter data, an educated guess (e.g., predicting the mean follower count for all inputs) can function as a satisfactory base model. In a more advanced scenario, you might want to compare your model against an existing state-of-the-art algorithm.
Determine the Success Criteria
We can use a performance metric to determine the success criteria. This will, in turn, allow us to validate the hypothesis (our model was better than the base model) or invalidate the hypothesis (our model was no better than the base model).
For regression analysis, typical performance metrics include:
- Mean Squared Error (MSE)
The average squared difference between the prediction a model produces and the values actually observed.Because MSE calculates the error value using squaring, the units of the error value are also squared. So, in the case of our Twitter experiment which uses "followers" as a unit, the error value that MSE produces would be "followers squared". This can get a little confusing when you're trying to wrap your head around it. - Root Mean Squared Error (RMSE)
The square root of the average squared difference between the prediction a model produces and the values actually observed.Because RMSE takes the square root of the squared error value, the square operations cancel out, and the end result uses the same units as the input data. This makes it easier to understand because you can compare it directly with the data. - Coefficient of Determination ([latex]r^2[/latex])
The amount of variance that can be explained by the model, i.e., how well does the model fit the data.Unless you're doing something unusual, the values for [latex]r^2[/latex] will be between 0 and 1, where 1 indicates that the model perfectly fits the test data.
For our experiment, we are going to use the RMSE and [latex]r^2[/latex] values as performance metrics.
We will calculate the RMSE and [latex]r^2[/latex] values for both the base model and our linear regression model. Comparing these values will allow us to determine which model is better, and can, therefore, be used to test our hypothesis.
Note: normally, when evaluating different machine learning models, more robust techniques (like k-fold cross-validation or statistical hypothesis tests) would be used to help choose the final model. But that is beyond the scope of this tutorial.
Identify the Independent and Dependent Variables
We have two types of variable:
- Independent variables essentially define the setup conditions for each prediction. They are called "independent" because they don't depend on anything—we get to choose them.
- Dependent variables are the results of each prediction. They're called "dependent" because they depend on independent variables we chose.
So, for us:
- Follower count and model are our independent variables because they reflect the scenario we're testing.
- The RMSE and [latex]r^2[/latex] scores are our dependent values because they reflect the performance characteristics of a specific scenario.
Define the Control Environment
The control environment is basically the setup we're planning to use for our independent variables.
For us, we're interested in comparing the actual following count vs. the predicted following account for every Twitter user in our data set. And we want to do this once each for both models: our base model and our linear regression model. No other variables will be changed between comparisons.
Load the Data
Now we've defined the crucial aspects of our experiment, we're ready to get our hands dirty with some actual code.
If you followed along with the instructions in the last part of this miniseries, you should have:
- A running CrateDB node
- Twitter test data
- A working Jupyter Notebook installation
- The ability to query to CrateDB from Jupyter Notebook
We're gonna use this setup to conduct our experiment.
To save you a bit of time: if you previously set up this environment, you can get things up and running again in three steps:
- Run
bin/cratefrom the CrateDB directory - Run
anaconda-navigator - Launch Jupyter Notebook
I have not included all the code necessary for running this experiment in this post. Instead, I will show the most important parts.
The full code is available on GitHub. If you want to follow along, you can download the reference notebook and use that to interact with your Twitter test data, using this blog post as a guide.
Clone the repository:
$ https://github.com/crate/cratedb-jupyter.gitOpen Jupyter Notebook (see the previous post) and use the file system browser to navigate to the cratedb-jupyter directory you just created.
You should see something like this:
Select CrateDB and Linear Regression.ipynb, and the notebook should open in a new tab:
Woo!
First things first. Let's set up the environment.
This notebook is a mix of explanatory text, code cells, and program output. A code cell is just a chunk of code.
Here are the first two cells:
Select the Run this cell icon that appears when you hover your mouse over In [1] in the left-hand margin. When you do, the [1] will increment, but nothing else will change because all we've done is import some modules so there is no output to display.
Repeat the process for the next cell. This sets some configuration values for the graphs we'll be producing later. Again, no output.
Take heed of the comments in the first cell before moving on. This is covered in the previous part of this miniseries. But in case you don't have the crate Python module installed, you must install it like so:
$ /anaconda3/bin/pip install crateNow we come to this cell:

This code:
- Defines an SQL query to fetch data from CrateDB
- Executes the query using pandas
- Displays the first five rows of the resultant
DataFrame
You should see something like this:
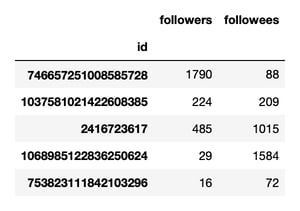
The specific values you see will differ from this screenshot because the tweets you imported were different from mine.
As you progress through this tutorial, the rest of your results will also be different. This provides you with an opportunity to interpret your own results.
Explore the Data
Before we go any further, let's plot the data we have using a scatter plot. Doing this allows us to explore the data.
Fortunately, with pandas, we can plot the data very easily:

When you execute, you should see a scatter plot:

Here, we see that some values are very large, but most of the data lies in the lower left-hand corner. (Yours may look a little different, but this observation probably still holds true.)
This isn't an ideal situation, because linear regression is very sensitive to outliers. All it takes is a couple of very large values to change our prediction model significantly.
Additionally, looking at this scatter plot, there doesn't appear to be a linear relationship between followees and followers.
Preprocess the Data
Before we continue, let's address the issues we have:
- A few very large outliers
- No apparent linear relationship
We can address both of these by transforming the input values. This just means that we apply a mathematical function to the data to transform it before we feed it to our machine learning model.
In particular, we can apply a nonlinear function to get a linear relationship:
[latex]f(x)[/latex]
Logarithms are a popular nonlinear function:
[latex]\log_b \, (x)[/latex]
Logarithms retain the original ordering of the data (e.g., large values remain large) while also "pulling in" outliers (i.e., making them less extreme). This behavior makes logarithms particularly suitable when the ratio of the smallest value to the largest value is very large—which is the case for our data!
So, let's apply a logarithmic function:
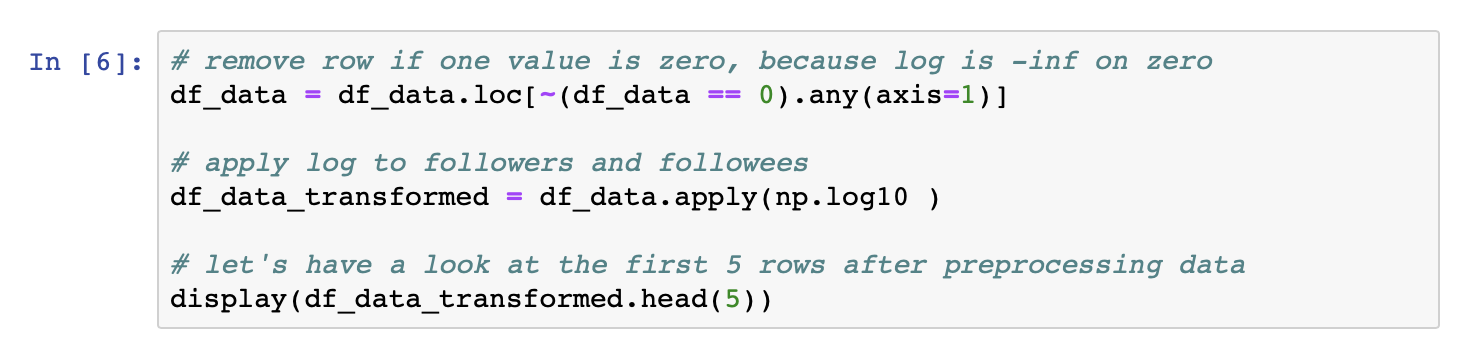
This code:
- Removes rows with zero values for followers and followees, since [latex]\log \, (0)[/latex] will return negative infinity
- Applies [latex]\log_{10} \, (x)[/latex] to both the followers and followees columns
- Displays the first five rows of the resultant
DataFrame
We could use [latex]\log_e \, (x)[/latex], but in practice most people prefer to use [latex]\log_{10} \, (x)[/latex] because it is easier to interpret.
If the value of [latex]\log_{10} \, (x)[/latex] increases by one, the value of [latex]x[/latex] increases by 10. In the case of [latex]\log_e \, (x)[/latex], [latex]x[/latex] would be increased by [latex]e[/latex], which is non-intuitive.
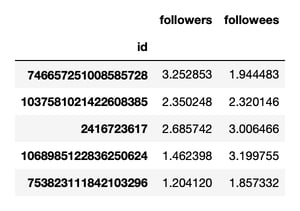
When you execute this cell, you should see a table like this:
Great! Let's plot it with this:

You should see a plot that looks like this:
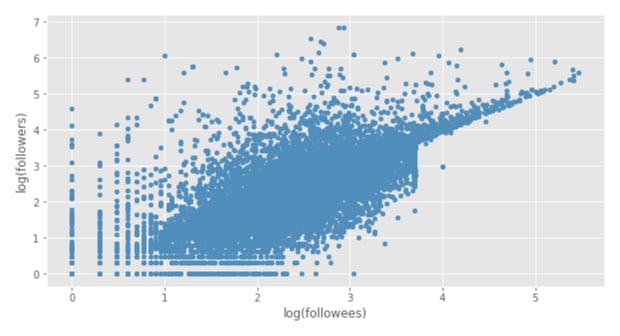
Huzzah!
Immediately, here, we can see the outline of a linear relationship between followees and followers (i.e. one increases as the other increases). We still have outliers, but they're less extreme, so they won't influence the model as much as before.
Now we can move on to building our models.
Establish a Base Model
Before we can start building our base model, we have to split the data into training and testing data:
- Training data is used to fit the models
- Test data is used to evaluate the trained models
With scikit-learn, we can randomly split the data into training (two thirds) and testing (one third) with a single line of code:

Now we have our training data, we can set up our base model by calculating the average number of followers:

Which, in my case, gave this:
'Average followers 2.429029322032724'Here, remember that we've applied a logarithmic function to the data. So, to get the real-world value this corresponds to, we have to apply:
[latex]10^x[/latex]
In my case, that's 269 followers.
So, our base model predicts 269 followers for all Twitter users.
Let's evaluate this model using the RMSE and [latex]r^2[/latex] values mentioned earlier:
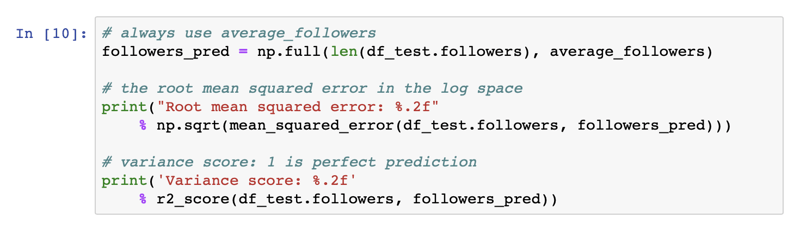
When I did this, I got the following result:
Root mean squared error: 0.86
Variance score: -0.00To find out what the RMSE score means, we can apply [latex]10^x[/latex] like before, which gives us 7.24435960075. This means that by predicting 269 followers over and over again, we can expect to be off by a factor of 7x. Eep! Not great. But we expected that.
The variance score ([latex]r^2[/latex]) is zero. Which again, is what we'd expect, because we guess the same value (~269 followers) no matter the input (followees), so there is no linear relationship between the input and output values.
Establish a Linear Regression Model
With our base model in hand, we can move on to the interesting stuff: creating and training a linear regression model.
Let's see if we can beat the base model and validate our hypothesis.
Execute this cell:

This code:
- Creates a linear regression model using the
LinearRegressionclass - Trains the model using the training data
With this in hand, we can use the LinearRegression class to predict the number of followers each use has:
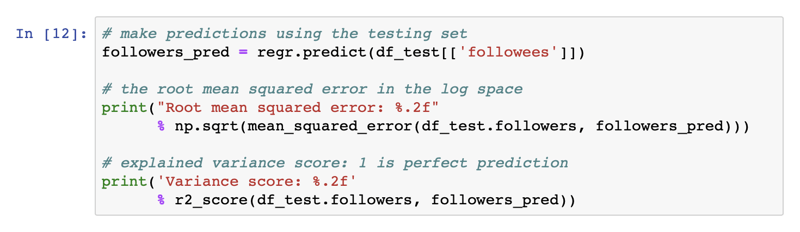
With my data, I got the following result:
Root mean squared error: 0.62
Variance score: 0.48Again, to find out what the RMSE score means, we can apply [latex]10^x[/latex], which gives us 4.1686938347. Which means can expect our predictions to be off by a factor of 4x. Which may not be perfect, but it is an improvement.
The variance score ([latex]r^2[/latex]) is a huge improvement over the base model. A variance score of zero means the model does not explain any of the variances, and a score of one indicates the model explains all of the variances.
In conclusion:
The changes in the respective performance scores support our hypothesis that the linear regression model performs better than the base model.
Nice!
But we can do better than that.
Let's visualize it.
Visualize the Linear Regression Model
Now that we have prediction data, we can plot this alongside the actual data:

Which gives us this:
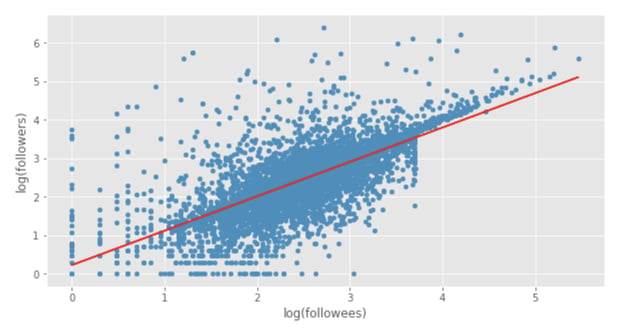
Here, the test data is plotted in blue, and the predictions of our linear regression model are plotted in red.
As before, the values on this plot represent logarithm values. If we want to access the non-logarithmic predictions, we have to apply a reverse transformation:

When I ran this, I saw the following:
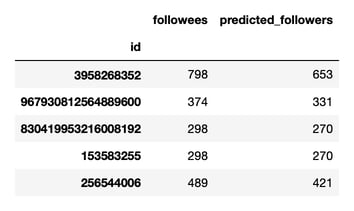
Cool.
Let's write the results back to CrateDB:

This code:
- Creates a new table named predicted_followers
- Inserts the predicted followers values
And, if you switch over to the CrateDB admin UI, you should see something like this:
Et voila!
Wrap Up
In this post we:
- Formulated the hypothesis that a linear regression model would outperform a naïve base model
- Loaded data into Jupyter Notebook from CrateDB and pre-processed it to help us visualize the linear relationship and limit the impact of outliers
- Made predictions using both models
- Calculated performance scores and consequently validated our hypothesis
I hope you enjoyed this miniseries. Hopefully, you feel more confident getting your feet wet with machine learning or data science more generally.
If you haven't already done so, check out part one for an introduction to machine learning and part two for an introduction to data science and working with CrateDB, Jupyter Notebook, and Pandas.
If you'd like me to cover something else in a follow-up post, please don't hesitate to drop me a line.